'프로그래밍' 카테고리의 다른 글
| Visual Studio Property Sheets를 이용해서 공통된 속성 관리하기 (0) | 2012.10.04 |
|---|---|
| 윈도우창 관련 메시지 정리 (0) | 2012.09.28 |
| Bullet 엔진 (0) | 2011.12.26 |
| Optimizing the Graphics Pipeline (0) | 2011.12.13 |
| 크라이엔진 SDK 무료 공개 (0) | 2011.08.18 |
| Visual Studio Property Sheets를 이용해서 공통된 속성 관리하기 (0) | 2012.10.04 |
|---|---|
| 윈도우창 관련 메시지 정리 (0) | 2012.09.28 |
| Bullet 엔진 (0) | 2011.12.26 |
| Optimizing the Graphics Pipeline (0) | 2011.12.13 |
| 크라이엔진 SDK 무료 공개 (0) | 2011.08.18 |
| SIMD를 이용한 수학 라이브러리 만들기 - 3. Vector 클래스 (0) | 2011.11.11 |
|---|---|
| SIMD를 이용한 수학 라이브러리 만들기 - 2. CPU 식별하기 (0) | 2011.11.10 |
| SIMD를 이용한 수학 라이브러리 만들기 - 1. SIMD란? (0) | 2011.11.07 |
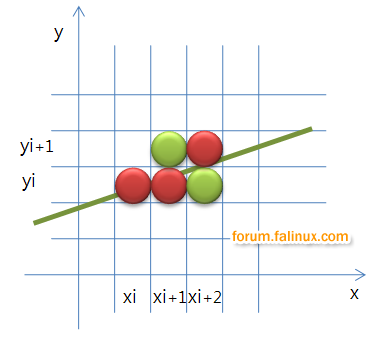
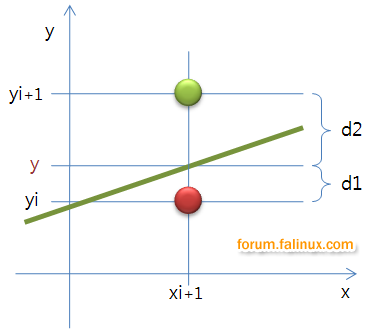
방정식에 의해 나온 y값이 정수값인 yi와 yi+1중 어디에 가까운지 판단하는 것 부터 아이디어를 뻗어나가면 된다.
위에 그림처럼 d1과 d2값을 구해 더 차이가 적은 쪽을 선택하면 된다.
직선의 방정식 : mx + b ( m은 기울기, b는 y절편 ) m = dy/dx
d1 = m(xi+1) + b - yi
d2 = (yi+1) - m(xi+1) - b
계산 한번으로 어디에 가까운지 판단하기 위해서 위 두 식을 합친다.
d1 - d2를 구해 이 값이 0보다 작다면 d1이 작다는 의미로 판단할 수 있고 0보다 크다면 d2가 더 작다는 것을 알 수 있다.
d1 - d2 = m(xi+1) + b - yi - ((yi+1) - m(xi+1) - b)
= m(xi+1) + b - yi - (yi+1) + m(xi+1) + b
= 2m(xi+1) + 2b - 2yi - 1
식을 x와 y값을 이용해서만 계산할 수 있게 하기위해 m = dy/dx를 넣어 정리해 준다.
d1 - d2 = 2(dy/dx)(xi+1) + 2b - 2yi - 1
해당 값의 부호만 판단하면 되기 때문에 굳이 코스트가 많이 드는 나누기 연산을 할 필요가 없다.
따라서 dx를 양변에 곱해준다.
dx(d1 - d2) = 2(dy)xi + 2dy + 2b(dx) - 2(dx)yi - dx
b, dx, dy값은 변화하지 않는 상수이므로 한번만 계산하면 된다.
위 식을 다시 이쁘게 정리해보자.
dx(d1 - d2) = 2(dy)xi - 2(dx)yi + 2dy - dx + 2b(dx)
= 2(dy)xi - 2(dx)yi + 2dy + dx(2b - 1)
위에 빨간색으로 밑줄친 부분은 선을 긋겠다고 마음 먹은 시점에 dx, dy, b값을 알 수 있기 때문에
계산을 하고 한 변수에 넣어 두면 된다. 식에서도 보기 쉽게 C로 정리하겠다.
dx(d1 - d2) = 2(dy)xi - 2(dx)yi + C
일단 1차적인 공식은 끝이 났다.
브레젠함 알고리즘은 이전 값을 이용하여 다음 값을 찾는 형식으로 루프를 돌게 되어있다.
이전 값을 Pi라 하고 그 이후의 값을 Pi+1이라 하자.
Pi = 2(dy)xi - 2(dx)yi + C
Pi+1 = 2(dy)xi+1 - 2(dx)yi+1 + C
이전 Pi값에 계속 값을 더해주어서 다음 값을 찾는 방법을 이용하기 때문에
더해주어야 되는 값을 구하기 위해 Pi+1 에서 Pi 를 빼보자.
Pi+1 - Pi = 2(dy)xi+1 - 2(dx)yi+1 + C - 2(dy)xi + 2(dx)yi - C
= 2(dy)(xi+1 - xi) - 2(dx)(yi+1 - yi)
지금은 dx가 dy보다 크다고 가정을 한 상태에서 식을 세우고 있기 때문에
xi+1 - xi = 1 이 된다. (무조건 한 칸씩 옆으로 가니까)
대신 y값은 이전과 같은 점일 수도 있고 한 칸 움직인 점일 수도 있다.
그렇기 때문에 위의 식에서 부터 두 가지 경우에 대한 식으로 정리할 수 있다.
1. yi+1 - yi = 0 일때 : 2(dy) -> Pi+1 = Pi + 2(dy)
2. yi+1 - yi = 1 일때 : 2(dy) - 2(dx) -> Pi+1 = Pi + 2(dy) - 2(dx)
이를 통해 다음 P값을 구할 수 있는 식을 구하게 되었다.
조건에 의해서 두 식중 알맞는 식을 골라서 사용해 나아가면 된다.
이런 점화식을 적용하기 위해서는 처음 값을 알아야 그 뒤부터 적용이 가능하다.
지금의 상황의 경우에는 처음 점을 (X1, Y1)으로 두고 그 다음 점을 (X1 + 1, Y1 + 1/2) 로 두고
구해내면 된다. (x는 1씩 증가하지만 y는 어떻게 될 지 모르기 때문에 절반 값을 넣어 줌)
위 점화식에 넣고 구해보면 최종적으로 처음 점은
P0 = 2(dy) - (dx)가 나온다.
지금까지 나온 값들을 적용해서 코드로 변경하면 된다.
| Cohen–Sutherland algorithm_Wiki (0) | 2012.08.16 |
|---|---|
| 소프트웨어 렌더링 공개 소스 코드 (0) | 2011.08.17 |
| Clear함수 구현 (0) | 2011.05.17 |
| 시작하기 (0) | 2011.05.16 |
| 소프트웨어 렌더링 참고 링크 (0) | 2011.05.13 |
비트맵에 렌더링을 할 때 이전에 그린 부분을 지워주고 다시 그리기 위해 Clear란 함수를 만든다.
일반적으로 게임을 만들때는 화면에 Clear해주는 배경색은 보이지 않는다.
하지만 Dx에서도 배경색을 설정하는 부분은 있으니 따라서 만들겠다.
일단 간단하게 생각해 볼 수 있는 것은 비트맵 사이즈만큼 루프를 돌면서 각각 픽셀을 원하는 색으로 칠해주는 것이다.
for (int y = 0; y < height_; ++y)
{
for (int x = 0;x < width_; ++x)
{
//SetPixel(x, y, color);
bits_[y * width_ + x] = color;
}
}
매 프레임마다 이런식으로 처리하게 되면 매우 느려진다. 처음에 테스트 삼아 이런식으로 구현해 봤는데
아무것도 안 그리고 Clear() 만 하는데도 FPS가 어마어마하게 떨어졌었다.
배열을 빨리 초기화해 주는 방법으로는 메모리 함수를 이용하는 것이 좋다.
memset()이나 memcpy()와 같은 함수들 말이다.
기존에 만들어진 memset()의 경우에는 1바이트 단위로 처리가 되기 때문에 현재 4바이트를 사용하는 비트맵을 초기화는
하지 못한다. (대신 검은색은 모든 바이트가 0이므로 가능하다.)
g-matrix소스를 참고 하니 위에 한줄을 갱신하고 각 줄마다 memcpy()를 이용하여 복사하는 구문이 있어서 사용해 봤는데
많은 속도 개선이 있었다.
for (int x = 0; x < width_ ; ++x)
{
bits_[x] = color;
}
for (int y = 1; y < height_ ; ++y)
{
memcpy(&(bits_[y * width_]), &(bits_[0]), sizeof(DWORD) * width_);
}
개인적인 생각으로는 어셈에 익숙해 지면 4바이트를 복사하는 memset() 함수를 만들 수 있을 것 같다.
일단 이 Clear() 함수를 사용하고 나중에 수정할 수 있으면 수정하겠다.
| Cohen–Sutherland algorithm_Wiki (0) | 2012.08.16 |
|---|---|
| 소프트웨어 렌더링 공개 소스 코드 (0) | 2011.08.17 |
| Bresenham 알고리즘을 이용한 선 그리기 (0) | 2011.05.21 |
| 시작하기 (0) | 2011.05.16 |
| 소프트웨어 렌더링 참고 링크 (0) | 2011.05.13 |
소프트웨어 렌더링을 구현하기 위해 처음으로 시작해야 할 것은 소프트웨어 렌더링을 할 환경을 만드는 일이다.
나는 비트맵 하나를 생성하고 비트맵에 렌더링을 한 뒤 최종적으로 Bitblt()을 통해 DC에 그려주는 식으로 만들었다.
비트맵을 관리하는 DIBSection이라는 클래스를 하나 만들고 사이즈와 비트맵이 그려질 DC를 넘겨주면
생성되는 식으로 만들었다.
그려줄 때는 비트맵이 그려질 DC에 비트맵과 연결된 메모리 DC를 그려주면 된다.
BitBlt(screenDC_, 0, 0, width_, height_, memoryDC_, 0, 0, SRCCOPY);
생성시에는 BITMAPINFO 구조체에 값을 설정하고 CreateDIBSection()함수를 통해 생성하였다.
BITMAPINFO bmInfo;
ZeroMemory(&bmInfo, sizeof(BITMAPINFO));
bmInfo.bmiHeader.biSize = sizeof(BITMAPINFOHEADER);
bmInfo.bmiHeader.biWidth = width_;
bmInfo.bmiHeader.biHeight = -height_; // 위에서 아래로 가는 좌표계로 사용하기 위해
bmInfo.bmiHeader.biPlanes = 1;
bmInfo.bmiHeader.biBitCount = DEFAULT_BPP; // 32비트로 만듦
bmInfo.bmiHeader.biCompression = BI_RGB;
bmInfo.bmiHeader.biSizeImage = 0;
bmInfo.bmiHeader.biXPelsPerMeter = 0;
bmInfo.bmiHeader.biYPelsPerMeter = 0;
bmInfo.bmiHeader.biClrUsed = 0;
bmInfo.bmiHeader.biClrImportant = 0;
bitmap_ = CreateDIBSection(memoryDC_, (BITMAPINFO *)&bmInfo, DIB_RGB_COLORS, (VOID **)&bits_, NULL, 0);
이후부터는 레스터라이저와 같은 클래스를 만들고 bits_ 배열에 접근하여 비트맵을 수정하면 된다.
bits_[y * width_ + x] = color;
다음에는 브레젠함 알고리즘을 이용한 선 그리기에 대해서 정리하겠다.
| Cohen–Sutherland algorithm_Wiki (0) | 2012.08.16 |
|---|---|
| 소프트웨어 렌더링 공개 소스 코드 (0) | 2011.08.17 |
| Bresenham 알고리즘을 이용한 선 그리기 (0) | 2011.05.21 |
| Clear함수 구현 (0) | 2011.05.17 |
| 소프트웨어 렌더링 참고 링크 (0) | 2011.05.13 |
참고 사이트
http://www.devmaster.net/articles.php - 소프트웨어 렌더링 뿐만 아니라 다양한 아티클들이 있음.
공개 엔진
http://www.g-matrix.pe.kr/ - 소프트웨어 렌더링 코드가 공개되어 있는 유명한 사이트
http://www.codeplex.com/Coco3D - 2D 라이브러리도 있던데 3D 라이브러리도 만들었나 봅니다.
지속적으로 추가할 예정..
| Cohen–Sutherland algorithm_Wiki (0) | 2012.08.16 |
|---|---|
| 소프트웨어 렌더링 공개 소스 코드 (0) | 2011.08.17 |
| Bresenham 알고리즘을 이용한 선 그리기 (0) | 2011.05.21 |
| Clear함수 구현 (0) | 2011.05.17 |
| 시작하기 (0) | 2011.05.16 |