반응형
Bresenham 알고리즘은 선 그리기를 할 때 내가 이번에 그릴 선이 어디 위치에 있는지 구하려면 실수 연산이 필요한데
이를 정수연산으로만 끝낼 수 없을까에서 나온 알고리즘이다.
실수연산이 정수연산에 비해서 매우 느린 것도 이유가 되고 어차피 화면에 그려질 때도 정수단위의 픽셀에 그려지기 때문에
정수연산만으로 처리하는 것이 더 좋다.
x의 변화량이 y의 변화량 보다 크다면
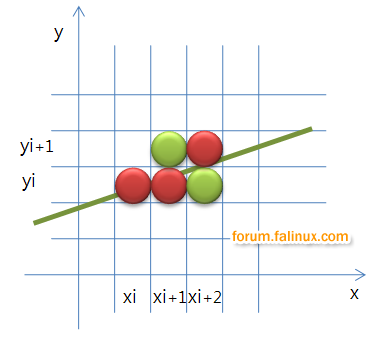
위와 같은 그림으로 그려지게 될 텐데 xi와 xi + 1까지는 y값이 yi에 더 가깝기 때문에 yi에 점이 그려지고
xi + 2때는 y값이 yi + 1에 더 가깝기 때문에 yi + 1에 그려져야 나름 부드럽게 보이는 선이 만들어지게 된다.
직선의 방정식 : mx + b ( m은 기울기, b는 y절편 ) m = dy/dx
d1 = m(xi+1) + b - yi
d2 = (yi+1) - m(xi+1) - b
계산 한번으로 어디에 가까운지 판단하기 위해서 위 두 식을 합친다.
d1 - d2를 구해 이 값이 0보다 작다면 d1이 작다는 의미로 판단할 수 있고 0보다 크다면 d2가 더 작다는 것을 알 수 있다.
d1 - d2 = m(xi+1) + b - yi - ((yi+1) - m(xi+1) - b)
= m(xi+1) + b - yi - (yi+1) + m(xi+1) + b
= 2m(xi+1) + 2b - 2yi - 1
식을 x와 y값을 이용해서만 계산할 수 있게 하기위해 m = dy/dx를 넣어 정리해 준다.
d1 - d2 = 2(dy/dx)(xi+1) + 2b - 2yi - 1
해당 값의 부호만 판단하면 되기 때문에 굳이 코스트가 많이 드는 나누기 연산을 할 필요가 없다.
따라서 dx를 양변에 곱해준다.
dx(d1 - d2) = 2(dy)xi + 2dy + 2b(dx) - 2(dx)yi - dx
b, dx, dy값은 변화하지 않는 상수이므로 한번만 계산하면 된다.
위 식을 다시 이쁘게 정리해보자.
dx(d1 - d2) = 2(dy)xi - 2(dx)yi + 2dy - dx + 2b(dx)
= 2(dy)xi - 2(dx)yi + 2dy + dx(2b - 1)
위에 빨간색으로 밑줄친 부분은 선을 긋겠다고 마음 먹은 시점에 dx, dy, b값을 알 수 있기 때문에
계산을 하고 한 변수에 넣어 두면 된다. 식에서도 보기 쉽게 C로 정리하겠다.
dx(d1 - d2) = 2(dy)xi - 2(dx)yi + C
일단 1차적인 공식은 끝이 났다.
브레젠함 알고리즘은 이전 값을 이용하여 다음 값을 찾는 형식으로 루프를 돌게 되어있다.
이전 값을 Pi라 하고 그 이후의 값을 Pi+1이라 하자.
Pi = 2(dy)xi - 2(dx)yi + C
Pi+1 = 2(dy)xi+1 - 2(dx)yi+1 + C
이전 Pi값에 계속 값을 더해주어서 다음 값을 찾는 방법을 이용하기 때문에
더해주어야 되는 값을 구하기 위해 Pi+1 에서 Pi 를 빼보자.
Pi+1 - Pi = 2(dy)xi+1 - 2(dx)yi+1 + C - 2(dy)xi + 2(dx)yi - C
= 2(dy)(xi+1 - xi) - 2(dx)(yi+1 - yi)
지금은 dx가 dy보다 크다고 가정을 한 상태에서 식을 세우고 있기 때문에
xi+1 - xi = 1 이 된다. (무조건 한 칸씩 옆으로 가니까)
대신 y값은 이전과 같은 점일 수도 있고 한 칸 움직인 점일 수도 있다.
그렇기 때문에 위의 식에서 부터 두 가지 경우에 대한 식으로 정리할 수 있다.
1. yi+1 - yi = 0 일때 : 2(dy) -> Pi+1 = Pi + 2(dy)
2. yi+1 - yi = 1 일때 : 2(dy) - 2(dx) -> Pi+1 = Pi + 2(dy) - 2(dx)
이를 통해 다음 P값을 구할 수 있는 식을 구하게 되었다.
조건에 의해서 두 식중 알맞는 식을 골라서 사용해 나아가면 된다.
이런 점화식을 적용하기 위해서는 처음 값을 알아야 그 뒤부터 적용이 가능하다.
지금의 상황의 경우에는 처음 점을 (X1, Y1)으로 두고 그 다음 점을 (X1 + 1, Y1 + 1/2) 로 두고
구해내면 된다. (x는 1씩 증가하지만 y는 어떻게 될 지 모르기 때문에 절반 값을 넣어 줌)
위 점화식에 넣고 구해보면 최종적으로 처음 점은
P0 = 2(dy) - (dx)가 나온다.
지금까지 나온 값들을 적용해서 코드로 변경하면 된다.
참고 : http://forum.falinux.com/zbxe/?mid=graphic&page=3&document_srl=406146&listStyle=&cpage
위 사이트에 정리가 잘 되어 있어서 올립니다.
이 사이트에서 사용한 그림들도 위 사이트에서 사용한 그림을 이용하였습니다.
문제가 된다면 삭제하겠습니다.
이를 정수연산으로만 끝낼 수 없을까에서 나온 알고리즘이다.
실수연산이 정수연산에 비해서 매우 느린 것도 이유가 되고 어차피 화면에 그려질 때도 정수단위의 픽셀에 그려지기 때문에
정수연산만으로 처리하는 것이 더 좋다.
x의 변화량이 y의 변화량 보다 크다면

위와 같은 그림으로 그려지게 될 텐데 xi와 xi + 1까지는 y값이 yi에 더 가깝기 때문에 yi에 점이 그려지고
xi + 2때는 y값이 yi + 1에 더 가깝기 때문에 yi + 1에 그려져야 나름 부드럽게 보이는 선이 만들어지게 된다.
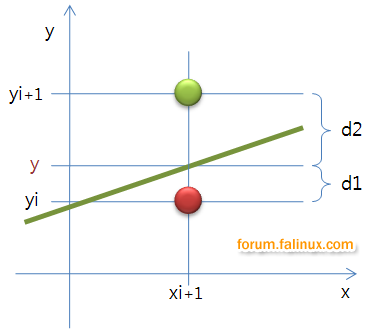
방정식에 의해 나온 y값이 정수값인 yi와 yi+1중 어디에 가까운지 판단하는 것 부터 아이디어를 뻗어나가면 된다.
위에 그림처럼 d1과 d2값을 구해 더 차이가 적은 쪽을 선택하면 된다.
직선의 방정식 : mx + b ( m은 기울기, b는 y절편 ) m = dy/dx
d1 = m(xi+1) + b - yi
d2 = (yi+1) - m(xi+1) - b
계산 한번으로 어디에 가까운지 판단하기 위해서 위 두 식을 합친다.
d1 - d2를 구해 이 값이 0보다 작다면 d1이 작다는 의미로 판단할 수 있고 0보다 크다면 d2가 더 작다는 것을 알 수 있다.
d1 - d2 = m(xi+1) + b - yi - ((yi+1) - m(xi+1) - b)
= m(xi+1) + b - yi - (yi+1) + m(xi+1) + b
= 2m(xi+1) + 2b - 2yi - 1
식을 x와 y값을 이용해서만 계산할 수 있게 하기위해 m = dy/dx를 넣어 정리해 준다.
d1 - d2 = 2(dy/dx)(xi+1) + 2b - 2yi - 1
해당 값의 부호만 판단하면 되기 때문에 굳이 코스트가 많이 드는 나누기 연산을 할 필요가 없다.
따라서 dx를 양변에 곱해준다.
dx(d1 - d2) = 2(dy)xi + 2dy + 2b(dx) - 2(dx)yi - dx
b, dx, dy값은 변화하지 않는 상수이므로 한번만 계산하면 된다.
위 식을 다시 이쁘게 정리해보자.
dx(d1 - d2) = 2(dy)xi - 2(dx)yi + 2dy - dx + 2b(dx)
= 2(dy)xi - 2(dx)yi + 2dy + dx(2b - 1)
위에 빨간색으로 밑줄친 부분은 선을 긋겠다고 마음 먹은 시점에 dx, dy, b값을 알 수 있기 때문에
계산을 하고 한 변수에 넣어 두면 된다. 식에서도 보기 쉽게 C로 정리하겠다.
dx(d1 - d2) = 2(dy)xi - 2(dx)yi + C
일단 1차적인 공식은 끝이 났다.
브레젠함 알고리즘은 이전 값을 이용하여 다음 값을 찾는 형식으로 루프를 돌게 되어있다.
이전 값을 Pi라 하고 그 이후의 값을 Pi+1이라 하자.
Pi = 2(dy)xi - 2(dx)yi + C
Pi+1 = 2(dy)xi+1 - 2(dx)yi+1 + C
이전 Pi값에 계속 값을 더해주어서 다음 값을 찾는 방법을 이용하기 때문에
더해주어야 되는 값을 구하기 위해 Pi+1 에서 Pi 를 빼보자.
Pi+1 - Pi = 2(dy)xi+1 - 2(dx)yi+1 + C - 2(dy)xi + 2(dx)yi - C
= 2(dy)(xi+1 - xi) - 2(dx)(yi+1 - yi)
지금은 dx가 dy보다 크다고 가정을 한 상태에서 식을 세우고 있기 때문에
xi+1 - xi = 1 이 된다. (무조건 한 칸씩 옆으로 가니까)
대신 y값은 이전과 같은 점일 수도 있고 한 칸 움직인 점일 수도 있다.
그렇기 때문에 위의 식에서 부터 두 가지 경우에 대한 식으로 정리할 수 있다.
1. yi+1 - yi = 0 일때 : 2(dy) -> Pi+1 = Pi + 2(dy)
2. yi+1 - yi = 1 일때 : 2(dy) - 2(dx) -> Pi+1 = Pi + 2(dy) - 2(dx)
이를 통해 다음 P값을 구할 수 있는 식을 구하게 되었다.
조건에 의해서 두 식중 알맞는 식을 골라서 사용해 나아가면 된다.
이런 점화식을 적용하기 위해서는 처음 값을 알아야 그 뒤부터 적용이 가능하다.
지금의 상황의 경우에는 처음 점을 (X1, Y1)으로 두고 그 다음 점을 (X1 + 1, Y1 + 1/2) 로 두고
구해내면 된다. (x는 1씩 증가하지만 y는 어떻게 될 지 모르기 때문에 절반 값을 넣어 줌)
위 점화식에 넣고 구해보면 최종적으로 처음 점은
P0 = 2(dy) - (dx)가 나온다.
지금까지 나온 값들을 적용해서 코드로 변경하면 된다.
참고 : http://forum.falinux.com/zbxe/?mid=graphic&page=3&document_srl=406146&listStyle=&cpage
위 사이트에 정리가 잘 되어 있어서 올립니다.
이 사이트에서 사용한 그림들도 위 사이트에서 사용한 그림을 이용하였습니다.
문제가 된다면 삭제하겠습니다.
반응형
'프로그래밍 > 소프트웨어 렌더링' 카테고리의 다른 글
| Cohen–Sutherland algorithm_Wiki (0) | 2012.08.16 |
|---|---|
| 소프트웨어 렌더링 공개 소스 코드 (0) | 2011.08.17 |
| Clear함수 구현 (0) | 2011.05.17 |
| 시작하기 (0) | 2011.05.16 |
| 소프트웨어 렌더링 참고 링크 (0) | 2011.05.13 |


