내적
벡터끼리의 곱 중에서 내적에 대해 알아보자.
참고로 외적에 대해서는 여기를 참고하자!
외적처럼 위키를 기준으로 정리하는 것이 아니라
이번에는 게임 프로그래밍 관련된 수학책을 참고하여 정리해보자.
게임 개발할때 많이 사용하기 때문에 관련된 부분만 정리해도 꽤 많은 분량이 될 것 같다.
벡터와 관련된 부분에 많이 사용되고 많이 사용되는 증거로 엔진 내의 수학 함수 뿐만 아니라
HLSL같은 쉐이더 등에서도 기본적으로 내적 연산 함수를 지원한다.
내적 연산
일단 영어로 내적은 dot product 혹은 inner product 라고 한다.
식으로 나타내면 \( a \cdot b \) 로 나타낼 수 있다. (dot!)
괄호가 쳐져있지 않는 한에는 벡터의 덧셈, 뺄셈보다 먼저 계산된다.
내적은 두 벡터의 각각 성분끼리의 곱의 합이다.
즉 스칼라값이 나온다는 것이다! (단순히 곱의 합이기 때문에 음수가 나올 수도 있다!)
식으로 표현하면 아래와 같다.
\( \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n-1 \\ a_n \end{bmatrix} \cdot \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n-1 \\ b_n \end{bmatrix} = a_1b_1 + a_2b_2 + \cdots + a_{n-1}b_{n-1} + a_nb_n \)
즉 \( a \cdot b = \sum_{i=1}^n a_ib_i \)
예를 들어 3차원 벡터끼리의 내적이면
\( a \cdot b = a_xb_x + a_yb_y + a_zb_z \)
기하하적 의미
첫번째로 알아볼 의미는 투영이다.

a벡터를 b벡터에 투영시키면 a1벡터가 된다.
만약에 b가 단위벡터라고 하면(길이가 1인 벡터 - 방향만 나타낸다고 보면 된다.)
a벡터가 b벡터로 내려꽂았을때의 결과이다. (위에서 빛을 비췄을떄 그림자가 진다고 생각하면 된다.)
주의해야 할 점은 내적계산을 하면 결과가 스칼라이기 때문에 투영된 길이만 의미한다는 것이다.
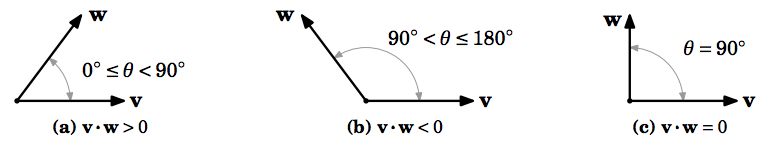
두 벡터가 이루는 각도에 따라서 위와 같이 부호가 결정된다.
예각일 경우에는 양수 / 90도일때는 0 / 둔각일 경우에는 음수가 된다.
다르게 말하면 주어진 벡터 2개의 성분만 알아도 두 벡터가 대충 어떤 방향을 바라보고 있는지 알아낼 수 있다는 것이다.
게임 개발에서 이는 매우 중요한 정보이다.
특정 면을 기준으로 앞쪽에 있는가 뒤에 있는가를 판단한다던가 그림자를 계산한다던가 다양한 부분에 사용할 수 있다.
만약 투영되는 벡터가 단위벡터가 아니라면 어떻게 될까?
\( a \cdot (\mathrm{k}b) = a_x(\mathrm{k}b_x) + a_y(\mathrm{k}b_y) + a_z(\mathrm{k}b_z) \)
\( = \mathrm{k}(a_xb+x + a_yb_y + a_zb_z) \)
\( = \mathrm{k}(a \cdot b) \)
단위벡터가 아니면 내적된 결과에 길이를 곱해주면 된다.
위에 식을 보면 알겠지만 k값이 어디로 옮겨가도 동일한 결과를 얻을 수 있다.
\( (\mathrm{k}a) \cdot b = \mathrm{k}(a \cdot b) = a \cdot (\mathrm{k}b) \)
그리고 곱셈과 덧셈이 교환법칙이 성립하기 때문에 내적 또한 교환 법칙이 성립한다.
\( a \cdot b = a_xb_x + a_yb_y + a_zb_z = b \cdot a \)
교환법칙을 본 김에 분배 법칙도 살펴보자.
\( \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} \cdot \begin{bmatrix} b_1 + c_1 \\ b_2 + c_2 \\ b_3 + c_3 \end{bmatrix} \)
\( = a \cdot (b + c) \)
\( = a_x(b_x + c_x) + a_y(b_y + c_y) + a_z(b_z + c_z) \)
\( = (a_xb_x + a_yb_y + a_zb_z) + (a_xc_x + a_yc_y + a_zc_z) \)
\( = a \cdot b + a \cdot c \)
역시나 곱셈과 덧셈으로 이루어진 연산이기 때문에 분배 법칙이 성립한다.
벡터가 -가 붙어도 결국에는 방향이 반대인 벡터를 더하는 것이기 때문에 마찬가지로 성립한다.
같은 벡터끼리 내적을 구하면 어떻게 될까?
\( v \cdot v = v_xv_x + v_yv_y + v_zv_z = v_x^2 + v_y^2 + v_z^2 = \lVert v \rVert ^2\)
\( \lVert v \rVert = \sqrt{v \cdot v} \)
바로 해당 벡터의 길이를 구할 수 있다!
다음은 투영된 벡터를 이용해서 수직 벡터를 구하는 것이다.

b벡터가 단위벡터라고 가정하자.
a1은 투영된 벡터 a2는 우리가 구하고 싶은 수직 벡터이다.
b벡터에 a벡터를 투영시킨 벡터는 아래와 같다.
\( a_1 = ( a \cdot b )b \)
내적값은 스칼라값이기 때문에 벡터를 곱해줘야 벡터가 된다.
벡터의 덧셈을 이용해보면
\( a_1 + a_2 = a \)
\( a_2 = a - a_1 \)
\( a_2 = a - ( a \cdot b)b \)
내적에 다른 의미

v 벡터가 단위벡터라고 했을때 투영된 벡터의 길이가 내적이였다.
위 그림을 다시 보면 u 벡터를 빗변 투영된 벡터를 밑변으로 하는 직각삼각형으로 볼 수 있다.
u벡터의 길이가 1이라면 내적값을 직각삼각형의 성질을 이용해 표현할 수 있지 않을까?
바로 코사인값으로 표현할 수 있다.
\( \cos\theta = {\text{밑변} \over \text{빗변}} \)
내적을 코사인으로 표현할 수 있다는 것을 알게되었다.

내적의 기하하적 의미에서 왜 예각일때 양수이고 90도일때 0이고 둔각일때 음수인지 이해할 수 있게 되었다.
바로 그것이 코사인의 성질이기 때문이다.
위에서 내적이 각 벡터의 길이에 비례한다는 것을 알았다.
식을 일반화 시키면 아래와 같다.
\( a \cdot b = \lVert a \rVert \lVert b \rVert \cos \theta \)
또한 코사인값이 나왔으니 반대로 코사인의 역함수를 사용하면 각도를 구할 수 있다는 것도 알 수 있다.
즉 두 벡터의 성분값만 알면 두 벡터가 어떤 각도로 배치되어 있는지도 알 수 있다는 것이다!
각도를 구해야될때 사용하면 되겠다.
\( \theta = \arccos(a \cdot b) \)
지금까지 벡터의 내적에 대해서 알아보았다.
여기 있는 내용을 기반으로 벡터에 대해서 점점 더 정리하면 될 것 같다.
참고자료
https://en.wikipedia.org/wiki/Vector_projection
http://jccc-mpg.wikidot.com/vector-projection
https://math.libretexts.org/TextMaps/Calculus_TextMaps/Map%3A_Vector_Calculus_(Corral)/1%3A_Vectors_in_Euclidean_Space/1.3%3A_Dot_Product
https://www.mathsisfun.com/algebra/trig-sin-cos-tan-graphs.html




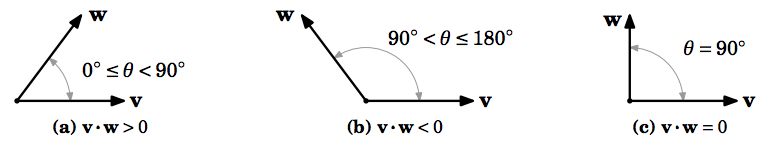





































 0, and it is
0, and it is








